Graph Knowledge
一些图论、图挖掘等图相关领域的知识收集、汇总。
节点相关的概念
degree 度
一个顶点的度(degree)指与该顶点关联的边的数目。当边有权重时,就是所有边的权重和。记做$deg(v)$。
在有向图中,还有出度(out-degree)和入度(in-degree)的概念。
出度(out-degree)指以该顶点为起点的边的权重和,入度(in-degree)指的是以该顶点为终点的边的权重和。
链接相关的概念
结构相关的概念
bipartite 二部
将图的顶点分成两个非空集合$V_1$和$V_2$,如果这个图的每一条边的两个端点都分别属于$V_1$和$V_2$,那么称这个图是二部图(bipartite)。
在这个概念的基础上,还有完全二部图(complete bipartite graph)的概念,指的是在 bipartite 的基础上,$V_1$中的每个点,都与$V_2$中的每个点相连。
graphlets 图元
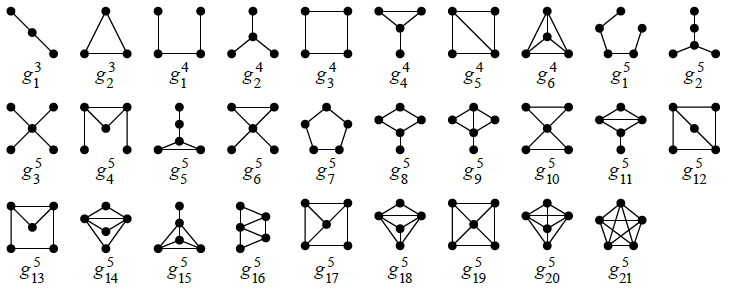
图元,指的是一系列异构的(_isomorphism_)导出(_induced_)子图。
下面列举所有的 3 节点、4 节点、5 节点的图元:
induced 导出
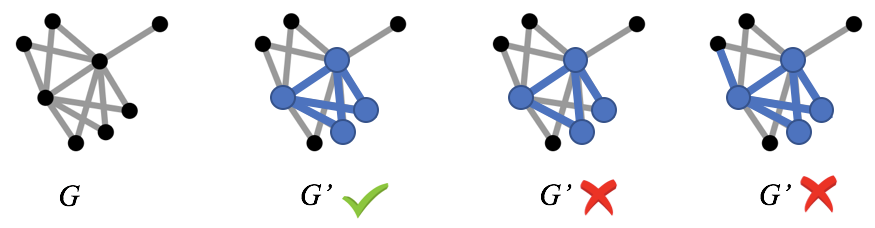
给定一个图$G$,以及这个图的子图(subgraph)$G’=(V’, E’)$,其中$V’\subseteq V$并且$E’ \subseteq E$。如果$E’ = \{(v_i,v_j)|(v_i,v_j) \in E \text{ and }v_i, v_j \in V’\}$,也就是对于所有属于$V’$的节点,他们在原图$G$的中出现的所有边,也都出现在$G’$的$E’$中,那么,这个子图$G’$称为$G$的导出(induced)子图。
下面是导出子图的一个示例:
isomorphism 同构
如果两个图$G = (V,E)$ 和 $G’ = (V’, E’)$ 之间存在一个双射(bijection)函数 $f: V \rightarrow V’$,使得$ (v_i, v_j) \in E \Leftrightarrow (f(v_i),f(v_j)) \in E’ \text{ for all }v_i,v_j \in V$,那么这两个图互为同构图(isomorphism)
subgraph 子图
给定一个图$G$,那么定义这个图的子图$G’=(V’, E’)$,其中$V’\subseteq V$并且$E’ \subseteq E$。
矩阵相关的概念
adjacency matrix 邻接矩阵
一个图的邻接矩阵的定义是:$A=\lbrace a_{ij} \rbrace$,其中$a_{ij}=e_{ij}$,第$ij$个元素指的是边$e_{ij}$的值。
incidence matrix 关联矩阵
一个图的关联矩阵定义为:$M=\lbrace m_{ij} \rbrace$,其中$m_{ij}$为 1,如果节点$v_i$和边$e_j$相关,举例而言:
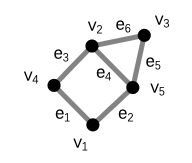
的关联矩阵为:
| e1 | e2 | e3 | e4 | e5 | e6 | |
|---|---|---|---|---|---|---|
| v1 | 1 | 1 | 0 | 0 | 0 | 0 |
| v2 | 0 | 0 | 1 | 1 | 0 | 1 |
| v3 | 0 | 0 | 0 | 0 | 1 | 1 |
| v4 | 1 | 0 | 1 | 0 | 0 | 0 |
| v5 | 0 | 1 | 0 | 1 | 1 | 0 |